Engineering Mathematics Objective Questions And Answers Pdf

If the difference between the mode and median is 2, then find the difference between the median and mean(in the given order).

Answer (Detailed Solution Below)

Option 2 : 1

Concept:

Relation between mode, median and mean is given by:

Mode = 3 × median – 2 × mean

Calculation:

Given:

Mode – median = 2

As we know

Mode = 3 × median – 2 × mean

Now, Mode = median + 2

⇒ (2 + median) = 3median – 2mean

⇒ 2Median - 2Mean = 2

⇒ Median - Mean = 1

∴ The difference between the median and mean is 1.

Consider the below data:

\(\begin{array}{*{20}{c}} x&:&0&1&2\\ {f\left( x \right)}&:&4&3&{12} \end{array}\)

The value of\(\mathop \smallint \nolimits_0^2 f\left( x \right)dx\) by Trapezoidal rule will be:

Answer (Detailed Solution Below)

Option 1 : 11

Concept:

Trapezoidal rule states that for a function y = f(x)

x	x0	x1	x2	x3	……	xn
y	y0	y1	y2	y3	……	yn

xn = x0 + nh, where n = Number of sub-intervals

h = step-size

\(\mathop \smallint \nolimits_{{x_0}}^{{x_0} + nh} f\left( x \right)dx = \frac{h}{2}\left[ {\left( {{y_0} + {y_n}} \right) + 2\left( {{y_1} + {y_2} + {y_3} + \ldots + {y_{n - 1}}} \right)} \right]\) ---(1)

For a trapezoidal rule, a number of sub-intervals must be a multiple of 1.

Calculation:

\(\begin{array}{*{20}{c}} x&:&0&1&2\\ {f\left( x \right)}&:&4&3&{12} \end{array}\)

Here: x₀ = 4, x₁ = 3, x₂ = 12, h = 1

From equation (1);

\(\mathop \smallint \limits_0^2 f\left( x \right)dx = \frac{h}{2}\left[ {\left( {{x_0} + {x_2}} \right) + 2\left( {{x_1}} \right)} \right]\)

\( = \frac{1}{2}\left[ {\left( {{4} + {12}} \right) + 2\left( {{3}} \right)} \right]={22\over2}=11\)

Key Points:

Apart from the trapezoidal rule, other numerical integration methods are:

Simpson's one-third rule:

For applying this rule, the number of subintervals must be a multiple of 2.

\(\mathop \smallint \nolimits_{{x_0}}^{{x_0} + nh} f\left( x \right)dx = \frac{h}{3}\left[ {\left( {{y_0} + {y_n}} \right) + 4\left( {{y_1} + {y_3} + {y_5} + \ldots + {y_{n - 1}}} \right) + 2\left( {{y_2} + {y_4} + {y_6} + \ldots + {y_{n - 2}}} \right)} \right]\) ..2)

Simpson's three-eighths rule:

For applying this rule, the number of subintervals must be a multiple of 3.

\(\mathop \smallint \nolimits_{{x_0}}^{{x_0} + nh} f\left( x \right)dx = \frac{{3h}}{8}\left[ {\left( {{y_0} + {y_n}} \right) + 3\left( {{y_1} + {y_2} + {y_4} + {y_5} + \ldots } \right) + 2\left( {{y_3} + {y_6} + \ldots } \right)} \right]\)

A bag contains 3 white, 2 blue and 5 red balls. One ball is drawn at random from the bag. What is the probability that the ball drawn is not red?

3/10
1/5
1/2
4/5

Answer (Detailed Solution Below)

Option 3 : 1/2

Calculation:

A bag contains 3 white, 2 blue and 5 red balls.

Total number of balls = 3 + 2 + 5 = 10

Number of balls that are not red = 10 - 5 = 5

Probability of balls drawn is not red = (number of balls which are not red)/(total number of balls) = 5/10 = 1/2

For what value of λ, do the simultaneous equation 2x + 3y = 1, 4x + 6y = λ have infinite solutions?

λ = 0
λ = 1
λ ≠ 2
λ = 2

Answer (Detailed Solution Below)

Option 4 : λ = 2

Concept:

Non-homogeneous equation of type AX = B has infinite solutions;

if ρ(A | B) = ρ(A) < Number of unknowns

Calculation:

Given:

2x + 3y = 1

4x + 6y = λ

The augmented matrix is given by:

\(\left( {A{\rm \ {|}} \ B} \right) = \left[ {\begin{array}{*{20}{c}} 2&3&{1\;}\\ 4&6&\lambda \end{array}} \right]\)

Applying R2 → R2 – 2R₁

\(\left( {A{\rm \ {|}} \ B} \right) = \left[ {\begin{array}{*{20}{c}} 2&3&{1\;}\\ 0&0&{\lambda - 2} \end{array}} \right]\)

For the system to have infinite solutions, the last row must be a fully zero row.

So if λ = 2 then the system of equations has infinitely many solutions.

Key Points:

Remember the system of equations

AX = B have

1) Unique solution, if ρ(A : B) = ρ(A) = Number of unknowns.

2) Infinite many solutions, if ρ(A : B) = ρ(A) < Number of solutions

3) No solution, if ρ(A : B) ≠ ρ(A).

The value of\(\mathop {\lim }\limits_{x \to 0} \left( {x\sin \frac{1}{x}} \right)\) is:

Answer (Detailed Solution Below)

Option 3 : 0

Concept:

sin θ can take from - ∞ to + ∞but sin θ gives - 1 to + 1, i.e. for values of θ from-∞ to+∞, sin θ always lies between -1 and 1.

\( - 1 \le \sin θ \le 1\)

sin ∞ gives finite value.

Analysis:

Let,

\(f(x)=\mathop {\lim }\limits_{x \to 0} \left( {x\sin \frac{1}{x}} \right)\)

When x = 0

f(x) = 0 × sin ∞

f(x) = 0 × Finite value

\(f(x)=\mathop {\lim }\limits_{x \to 0} \left( {x\sin \frac{1}{x}} \right)=0\)

The differential equation 2y dx – (3y – 2x) dy = 0 is

exact and homogenous but not linear
exact, homogenous and linear
exact and linear but not homogenous
homogenous and linear but not exact

Answer (Detailed Solution Below)

Option 2 : exact, homogenous and linear

Concept:

Homogenous equation: If the degree of all the terms in the equation is the same then the equation is termed as a homogeneous equation.

Exact equation: The necessary and sufficient condition of the differential equation M dx + N dy = 0 to be exact is:

\(\frac{{\partial M}}{{\partial y}} = \frac{{\partial N}}{{\partial x}}\)

Linear equation: A differential equation is said to be linear if the dependent variable and its differential coefficient only in the degree and not multiplied together.

The standard form of a linear equation of the first order, commonly known as Leibnitz's linear equation is:

\(\frac{{dy}}{{dx}}+Py=Q\)

where, P, Q is a function of x.

or,\(\frac{{dx}}{{dy}}+Px=Q\)

where, P, Q is a function of x.

Condition 1:

2y dx + (2x - 3y) dy = 0 ---.(1)

(It is Homogeneous)

Condition 2:

Equation (1) can be written as \(\frac{{dy}}{{dx}}=\frac{{2y}}{{2x\;-\;3y}}\) .

It is not a linear form.

or\(\frac{{dx}}{{dy}}=\frac{{2x-3y}}{{2y}}\)

\(\frac{{dx}}{{dy}}+\frac{{x}}{{y}}=\frac{{3}}{{2}}\)

It is in linear form

Condition 3:

M dx + N dy = 0

2y dx – (3y – 2x) dy = 0

hence, M = 2y and N = 2x - 3y

\(\frac{{\partial M}}{{\partial y}} =\frac{{\partial (2y)}}{{\partial y}}= 2\) and\(\frac{{\partial N}}{{\partial x}}= \frac{{\partial (2x+3y)}}{{\partial x}}=2\)

As\(\frac{{\partial M}}{{\partial y}}=\frac{{\partial N}}{{\partial y}}\)

so, it is an exact equation.

The standard ordered basis of R³ is {e₁, e₂, e₃} Let T : R³ → R³ be the linear transformation such that T(e₁) = 7e₁ - 5e₃, T (e₂) = -2e₂ + 9e₃, T(e₃) = e₁ + e₂ + e₃. The standard matrix of T is:

\(\left( {\begin{array}{*{20}{c}} 7&0&1\\ 0&{ - 2}&1\\ { - 5}&9&1 \end{array}} \right)\)
\(\left( {\begin{array}{*{20}{c}} 7&-2&1\\ -5&{ 9}&1\\ { 0}&0&1 \end{array}} \right)\)
\(\left( {\begin{array}{*{20}{c}} 7&0&-5\\ 0&{ - 2}&9\\ 1&1&1 \end{array}} \right)\)
\(\left( {\begin{array}{*{20}{c}} 7&-5&0\\ -2&{ 9}&1\\ { 1}&1&1 \end{array}} \right)\)

Answer (Detailed Solution Below)

Option 1 : \(\left( {\begin{array}{*{20}{c}} 7&0&1\\ 0&{ - 2}&1\\ { - 5}&9&1 \end{array}} \right)\)

Concept:

Matrix transformations:

Theorem: Suppose L: Rⁿ → R^m is a linear map. Then there exists an m×n matrix A such that L(x) = Ax for all x ∈ Rⁿ. Columns of A are vectors L(e₁), L(e₂), . . . , L(e_n), where e₁, e₂, . . . , e_n is the standard basis for R_n.

Calculation:

Given linear transformation are:

T(e1) = 7e1 - 5e3,

T(e2) = -2e2 + 9e3,

T(e3) = e1 + e2 + e3

Let the standard matrix be A with respect to the basis e1, e2, e3,

Now T(e1) = 7e1 + 0e₂ - 5e3,

T(e2) = 0e₁ -2e2 + 9e3,

T(e3) = e1 + e2 + e3.

The standard matrix will be (transpose of linear combinations)

\(\left( {\begin{array}{*{20}{c}} 7&0&1\\ 0&{ - 2}&1\\ { - 5}&9&1 \end{array}} \right)\)

The value of\(\mathop \smallint \nolimits_0^{2\pi } \mathop \smallint \nolimits_0^{\pi /4} \mathop \smallint \nolimits_0^1 {r^2}\sin \theta dr\;d\theta \;d\phi \) will be:

\(\frac{{\sqrt 2{\pi } }}{3}\left( {\sqrt 2 + \sqrt 3 } \right)\)
\(\frac{{{2\pi } }}{3}\left( {\sqrt 3 -1 } \right)\)
\(\frac{{ {2\pi } }}{3}\left( {\sqrt 2 - \sqrt 3 } \right)\)
\(\frac{{\sqrt 2{\pi } }}{3}\left( {\sqrt 2 -1 } \right)\)

Answer (Detailed Solution Below)

Option 4 : \(\frac{{\sqrt 2{\pi } }}{3}\left( {\sqrt 2 -1 } \right)\)

\(\mathop \smallint \nolimits_0^{2\pi } \mathop \smallint \nolimits_0^{\pi /4} \mathop \smallint \nolimits_0^1 {r^2} \sin \theta drd\theta d\phi \)

=\( \mathop \smallint \limits_0^{2\pi } \mathop \smallint \limits_0^{\frac{\pi }{4}} \mathop \smallint \limits_0^1 \left( {{r^2} \times dr} \right) \times \sin \theta d\theta d\phi \)

=\(\mathop \smallint \limits_0^{2\pi } \mathop \smallint \limits_0^{\frac{\pi }{4}} \left[ {\frac{{{r^3}}}{3}} \right]_0^1 \times \sin \theta d\theta d\phi \)

=\( \frac{1}{3}\mathop \smallint \limits_0^{2\pi } \mathop \smallint \limits_0^{\frac{\pi }{4}} \sin \theta \times d\theta \times d\phi \)

=\(\frac{1}{3}\mathop \smallint \limits_0^{2\pi } - \left[ {\cos \theta } \right]_0^{\frac{\pi }{4}} \times d\phi \)

=\( \frac{1}{3}\mathop \smallint \limits_0^{2\pi } - \left[ {\frac{1}{{\sqrt 2 }} - 1} \right] \times d\phi \)

=\(\frac{1}{{3\sqrt 2 }}\left[ {\sqrt 2 \phi - \phi } \right]_0^{2\pi }\)

=\(\frac{{2\pi }}{{3\sqrt 2 }}\left[ {\sqrt 2 - 1} \right]\)

=\(\frac{{\sqrt 2{\pi } }}{3}\left( {\sqrt 2 -1 } \right)\)

A complete solution of partial differential equation\(\frac {\partial z}{\partial x} - 3x^2 = \left(\frac {\partial z}{\partial y}\right)^2 - y\) will be ________, where a and b are arbitrary constants.

z² = ax² + by² + 1
\(z = ax + x^3 + \left(\frac 2 3\right) (a + y)^{\frac 3 2} + b\)
z^{1 / 2} = (x + a)^{1 / 2} + (y + b)^{1 / 2}
z = (ax² + by²)^{3 / 2} + 2

Answer (Detailed Solution Below)

Option 2 : \(z = ax + x^3 + \left(\frac 2 3\right) (a + y)^{\frac 3 2} + b\)

Concept:

Separable equation of the form f(x, p) = g(y, q)

Let f(x, p) = g(y, q) = a (constant)

Solve f(x, p) = a and g(y, q) = a for p and q, we get

p = ϕ(x, a) and q = ψ(y, a)

We have dz = p dx + q dy

Bu integration, we get the required solution as follows,

z = ∫ ϕ(x, a) dx + ∫ ψ(y, a) dy + b

Where a, b are arbitrary constants.

Calculation:

Given Partial differentiation equation is\(\frac {\partial z}{\partial x} - 3x^2 = \left(\frac {\partial z}{\partial y}\right)^2 - y\)

Writing in terms of p,q ⇒ p - 3x² = q² - y

Let p - 3x2 = q2 - y = a (constant)

Now p - 3x2 = a ⇒ p = 3x2 + a

q2 - y = a ⇒\(q = \sqrt {y+a}\)

Substituting the values of p and q in dz = p dx + q dy, we get

\(dz = (a+3x^2)dx + (\sqrt {y+a})dy \)

Integrating on both sides, we get the general solution as

\(z = ax + x^3 + \left(\frac 2 3\right) (a + y)^{\frac 3 2} + b\)

For the curve xy³ - yx³ = 6, the slope of the tangent line at the point (1, -1) is:

1 / 2
-1
2
1

Answer (Detailed Solution Below)

Option 2 : -1

Concept :

Let y = f(x) be the equation of a curve, then the slope of the tangent at any point say (x1, y1) is given by:

\(m = {\left[ {\frac{{dy}}{{dx}}} \right]_{\left( {{x_1},\;\;{y_1}} \right)}}\)

Calculation:

Given curve is xy3 - yx3 = 6

Now by partially differentiating the equation of curve with respect to x we get;

\(3xy^2\frac{dy}{dx}+y^3-3x^2y-x^3\frac{dy}{dx}=0\)

\(\frac{dy}{dx}({3xy^2-x^3})={3x^2y-y^3}\)

\(\frac{dy}{dx}=\frac{3x^2y-y^3}{3xy^2-x^3}\)

\(\frac{dy}{dx}=\frac{y(3x^2-y^2)}{x{(3y^2-x^2)}}\)

The slope(m) i.e. dy/dx of the tangent at (1, -1) is:

m = -1

A partial differential equation derived from the equation z = ae^by sinbx will be:

\(\frac{{\partial z}}{{\partial y}} = 2y{\left( {\frac{{\partial z}}{{\partial x}}} \right)^2}\)
\(\left( {1 + \frac{{\partial z}}{{\partial y}}} \right)\frac{{\partial z}}{{\partial x}} = z\)
\(\frac{{{\partial ^2}z}}{{\partial {x^2}}} + \frac{{{\partial ^2}z}}{{\partial {y^2}}} = 0\)
\(2z = x\frac{{\partial z}}{{\partial x}} + y\frac{{\partial z}}{{\partial y}}\)

Answer (Detailed Solution Below)

Option 3 : \(\frac{{{\partial ^2}z}}{{\partial {x^2}}} + \frac{{{\partial ^2}z}}{{\partial {y^2}}} = 0\)

z = aeby sinbx

Now by differentiating w.r.t. x we get:

\(\frac{{\partial z}}{{\partial x}} = a \times {e^{by}} \times \cos bx \times b\)

Again differentiating:

\( \frac{{{\partial ^2}z}}{{\partial {x^2}}} = - a \times {b^2} \times {e^{by}} \times \sin bx\) ----(1)

z = aeby sinbx

Now by differentiating w.r.t. y we get:

\(\frac{{\partial z}}{{\partial y}} = a \times \sin bx \times {e^{by}} \times b\)

Again differentiating:

\( \frac{{{\partial ^2}z}}{{\partial {y^2}}} = a \times {b^2} \times {e^{by}} \times \sin bx\) ----(2)

Now by adding (1) and (2) we get:

\(\frac{{{\partial ^2}z}}{{\partial {x^2}}} + \frac{{{\partial ^2}z}}{{\partial {y^2}}} = 0\)

Hence, Option 3 is correct.

If Rank (A) = 2 and Rank (B) = 3 then Rank (AB) is:

6
5
3
Data inadequate

Answer (Detailed Solution Below)

Option 4 : Data inadequate

Concept:

Rank:

The rank of a matrix is a number equal to the order of the highest order non-vanishing minor, that can be formed from the matrix.

For matrix A,it is denoted by ρ(A).

The rank of a matrix is said to be r if,

There is at least one non-zero minor of order r.
Every minor of matrix Ahaving order higher than r is zero.

Property of Rank of Matrix:

ρ(AB) ≤ min [ρ(A), ρ(B)]

Calculation:

Given:

ρ(A) = 2, ρ(B) = 3

Using properties

ρ(AB) ≤ min [ρ(A), ρ(B)]

ρ(AB) ≤ min (2,3)

⇒ ρ(AB) ≤ 2

Alternate Method

Let order of matrix A be 2 × m and order of matrix B be m × 3 (∵ for multiplication we need the column of A and row of B to be same)

∴ Order of matrix AB will be 2 × 3

Using properties

ρ(AB) ≤ min (Row, Column)

⇒ ρ(AB) ≤ min (2, 3) [only when the column of A and row of B is the same]

⇒ ρ(AB) ≤ 2.

∵ we don't know the dimension of A and B, we cannot predict the exact rank of AB but its maximum rank will be 2.

Important Points

Other properties of rank of a matrix are:

The rank of a matrix does not change by elementary transformation, we can calculate the rank by changing the matrix into Echelon form. In the Echelon form, the rank of a matrix is the number of non-zero rows of the matrix.
The rank of a matrix is zero if the matrix is null.
ρ(A) ≤ min (Row, Column)
ρ(AB) ≤ min [ρ(A), ρ(B)]
ρ(ATA) = ρ(A AT) = ρ(A) = ρ(AT)
If A and B are matrices of the same order, then ρ(A + B) ≤ ρ(A) + ρ(B) and ρ(A - B) ≥ ρ(A) - ρ(B).
If Aθis the conjugate transpose of A, then ρ(Aθ) = ρ(A) and ρ(A Aθ) = ρ(A).
The rank of a skew-symmetric matrix cannot be one.

The value of x for which of the following series converges is

\(x - \frac{{{x^2}}}{2} + \frac{{{x^3}}}{3} - \frac{{{x^4}}}{4} + \frac{{{x^5}}}{5} - \ldots \infty ,\)

The series converges f0r -1< x< 1
The series converges for -1 < x< 1
The series diverges for -1 < x < 1
The series converges for x > 1

Answer (Detailed Solution Below)

Option 2 : The series converges for -1 < x

Explanation:

Given series is,

\(x - \frac{{{x^2}}}{2} + \frac{{{x^3}}}{3} - \frac{{{x^4}}}{4} + \frac{{{x^5}}}{5} - \ldots \infty ,\)

\({u_n} = {\left( { - 1} \right)^{n - 1}}\frac{{{x^n}}}{n}\)

\({u_{n + 1}} = {\left( { - 1} \right)^n}\frac{{{x^{n + 1}}}}{{n + 1}}\)

\(\frac{{{u_{n + 1}}}}{{{u_n}}} = \frac{{ - n}}{{n + 1}}x\)

\(\mathop {{\rm{lt}}}\limits_{n \to \infty } \left| {\left. {\frac{{{u_n} + 1}}{{{u_{n\;\;}}}}} \right| = \mathop {{\rm{lt}}}\limits_{n \to \infty } \left( {\frac{n}{{n + 1}}} \right)\left( {\left| x \right|} \right)} \right.\)

\(= \left| x \right|\)

By ratio test, the given series converges for |x| < 1 and diverges for |x| > 1

Let us examine the series for x = ± 1

For x = 1, the series reduces to

\(1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} + \ldots\)

This is an alternating series and is convergent.

For x = -1 the series becomes

\(- \left( {1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \ldots } \right)\)

This is a divergent series as can be seen by comparison with P-series with P = 1

Hence the given series is converges for -1 < x

The value of\(\mathop {\lim }\limits_{x \to 2} \frac{{{x^2} - 4}}{{3x - 6}}\) is:

\(\frac1 3\)
\(\frac 4 3\)
1
\(\frac 2 3\)

Answer (Detailed Solution Below)

Option 2 : \(\frac 4 3\)

Concept :

L-Hospital Rule: Let f(x) and g(x) be two functions

Suppose that we have one of the following cases,

I.\(\mathop {\lim }\limits_{{\rm{x}} \to {\rm{a}}} \frac{{{\rm{f}}\left( {\rm{x}} \right)}}{{{\rm{g}}\left( {\rm{x}} \right)}} = \frac{0}{0}\)

II.\(\mathop {\lim }\limits_{{\rm{x}} \to {\rm{a}}} \frac{{{\rm{f}}\left( {\rm{x}} \right)}}{{{\rm{g}}\left( {\rm{x}} \right)}} = \frac{\infty }{\infty }\)

Then we can apply L-Hospital Rule ⇔\(\mathop {\lim }\limits_{{\bf{x}} \to {\bf{a}}} \frac{{{\bf{f}}\left( {\bf{x}} \right)}}{{{\bf{g}}\left( {\bf{x}} \right)}} = \mathop {\lim }\limits_{{\bf{x}} \to {\bf{a}}} \frac{{{\bf{f}}'\left( {\bf{x}} \right)}}{{{\bf{g}}'\left( {\bf{x}} \right)}}\)

Calculation:

Given:

\(\mathop {\lim }\limits_{x \to 2} \frac{{{x^2} - 4}}{{3x - 6}}\)

As we can see,\(\mathop {\lim }\limits_{x \to 2} \frac{{{x^2} - 4}}{{3x - 6}}=\frac{0}{0}\)

So, Apply the L-Hospital rule here,

\(\mathop {\lim }\limits_{x \to 2} \frac{{{2x} }}{{3}}\)

After putting the limit we'll get:

\(\mathop {\lim }\limits_{x \to 2} \frac{{{2x} }}{{3}}=\frac{4}{3}\)

Hence the required value of the limit is\(\frac4 3\).

\(\mathop {\lim }\limits_{x \to 0} \frac{{\cos x - 1}}{{\sin x - x}}\) is equal to

Undefined
∞
1
0

Answer (Detailed Solution Below)

Option 2 : ∞

Concept:

L-Hospital Rule: Let f(x) and g(x) be two functions

Suppose that we have one of the following cases,

I.\(\mathop {\lim }\limits_{{\rm{x}} \to {\rm{a}}} \frac{{{\rm{f}}\left( {\rm{x}} \right)}}{{{\rm{g}}\left( {\rm{x}} \right)}} = \frac{0}{0}\)

II.\(\mathop {\lim }\limits_{{\rm{x}} \to {\rm{a}}} \frac{{{\rm{f}}\left( {\rm{x}} \right)}}{{{\rm{g}}\left( {\rm{x}} \right)}} = \frac{\infty }{\infty }\)

Then we can apply L-Hospital Rule as:

\(\mathop {\lim }\limits_{{\bf{x}} \to {\bf{a}}} \frac{{{\bf{f}}\left( {\bf{x}} \right)}}{{{\bf{g}}\left( {\bf{x}} \right)}} = \mathop {\lim }\limits_{{\bf{x}} \to {\bf{a}}} \frac{{{\bf{f}}'\left( {\bf{x}} \right)}}{{{\bf{g}}'\left( {\bf{x}} \right)}}\)

Calculation:

Given:

\(\mathop {{\rm{lim}}}\limits_{x \to 0} \frac{{cos\;x\; -\;1}}{{sin\;x\; - \;x}} = \left( {\frac{0}{0}} \right)\) form

Applying L' Hospital rule:

\(\mathop {{\rm{lim}}}\limits_{x \to 0} \frac{{cos\;x - 1}}{{sin\;x-\;x}} =\mathop {{\rm{lim}}}\limits_{x \to 0} \frac{\frac{d}{dx}({cos\;x\; -\;1})}{{\frac{d}{dx}(sin\;x\;-\;x})} =\mathop {\lim }\limits_{{\rm{x}} \to 0} \frac{{-sin\;x {\rm{}}}}{{\cos {\rm{x}\;-\;1}}} \)

\(\mathop {\lim }\limits_{{\rm{x}} \to 0} \frac{{-sin\; {\rm{x}}}}{{\cos {\rm{x}\,-1\;}}} = \left( {\frac{0}{0}} \right){\rm{form}}\)

Once again by L' Hospital rule,

\({\rm{}}\mathop {\lim }\limits_{{\rm{x}} \to 0} \frac{{-cos\; {\rm{x}}}}{{{\rm{-sin~x}}}} = \frac{-1}{0} = \infty{\rm{}}\)

The general solution of partial differential equation

\(x\left( {{y^2} + z} \right)\frac{{\partial z}}{{\partial x}} - y\left( {{x^2} + z} \right)\frac{{\partial z}}{{\partial y}}=\left( {{x^2} - {y^2}} \right)z\) will be:

φ(xyz, x² + y² - 2z) = 0, where φ is an arbitrary function.
φ(x + y + z,x² + y²) = 0, where φ is an arbitrary function.
φ(x² + y² + z², x + y + z) = 0 where φ is an arbitrary function
φ(x + y - z, xy + yz + zx) = 0, where φ is an arbitrary function

Answer (Detailed Solution Below)

Option 1 : φ(xyz, x² + y² - 2z) = 0, where φ is an arbitrary function.

Concept:

Linear Partial Differential Equation of First Order:A linearpartial differential equationof the first order, commonly known as Lagrange's Linear equation, is of the form Pp + Qq = R where P, Q, and R are functions of x, y, z. This equation is called a quasi-linear equation.

Thus, to solve the equation of the form Pp + Qq = R, we have to follow this solution procedure:

1) Form the subsidiary equations as:

\(\frac {dx}{P} = \frac {dy}{Q} = \frac {dz}{R}\)

2) Solve any two simultaneous equations by any method giving u = a and v = b as its solutions.

3) Write the complete solution as φ (u, v) = 0 or u = f (v).

Lagrange's method of multipliers:

Consider the partial differentiation equation Pp + Qq = R

then auxiliary equations are given by:

\(\frac {dx}{P} = \frac {dy}{Q} = \frac {dz}{R}\)

Now choose multipliers P₁, Q₁, R₁ in such a way that in ratio

\(\frac {{{P_1}{dx}}+{{Q_1}{dy}}+{{R_1}{dz}}}{{{P_1}{P}}+{{Q_1}{Q}}+{{R_1}{R}}}\), denominators vanish.

⇒ P₁ dx + Q₁ dy + R₁ dz = 0

By integration, the solution is given by u (x, y, z) = c₁

Similarly, by choosing another set of multipliers, function v(x, y, z) is determined.

Then complete solution is given by f (u, v) = 0.

Calculation:

Given:

\(x\left( {{y^2} + z} \right)\frac{{\partial z}}{{\partial x}} - y\left( {{x^2} + z} \right)\frac{{\partial z}}{{\partial y}}=\left( {{x^2} - {y^2}} \right)z\)

Comparing with Pp + Qq = R,

P = x (y² + z); Q = -y (x² + z); R = (x² - y²) z;

∴ The auxiliary equations are:

\(\frac{{{\rm{dx}}}}{{{\rm{x\;}}\left( {{\rm{y^2}} + {\rm{z}}} \right){\rm{\;}}}} = \frac{{{\rm{dy}}}}{{{\rm{\;-y\;}}\left( {{\rm{x^2}} + {\rm{z}}} \right){\rm{\;}}}} = \frac{{{\rm{dz}}}}{{{\rm{z\;}}\left( {{\rm{x^2}} - {\rm{y^2}}} \right)}}\)

1^st function:

Using multipliers x, y and -1 ⇒

\({\rm{\;}}\frac{{{\rm{xdx}} + {\rm{ydy}} - {\rm{dz}}}}{{{\rm{x^2\;}}\left( {{\rm{y^2}} + {\rm{z}}} \right) - {\rm{\;y^2\;}}\left( {{\rm{x^2}} + {\rm{z}}} \right) - {\rm{z\;}}\left( {{\rm{x^2}} - {\rm{y^2}}} \right)}} = \frac{{{\rm{xdx}} + {\rm{ydy}} - {\rm{dz}}}}{0}\)

∴ x dx + y dy - dz = 0 ⇒ x² + y² - 2z = constant;

2^nd function:

Using multipliers 1/x, 1/y and 1/z

⇒\({\rm{\;}}\frac{{{\rm{{\frac{1}{x}}dx}} + {\rm{{\frac{1}{y}}dy}} + {\rm{{\frac{1}{z}}dz}}}}{{\left( {{\rm{y^2}} + {\rm{z}}} \right) - \left( {{\rm{x^2}} + {\rm{z}}} \right) + \left( {{\rm{x^2}} - {\rm{y^2}}} \right)}} \)

\(= \frac{{{\rm{{\frac{1}{x}}dx}} + {\rm{{\frac{1}{y}}dy}} + {\rm{{\frac{1}{z}}dz}}}}{0}\)

∴\({{\rm{{\frac{1}{x}}dx}} + {\rm{{\frac{1}{y}}dy}} + {\rm{{\frac{1}{z}}dz}}} = 0 \)

xyz = constant

So both the equations are:

x2 + y2 - 2z = constant; xyz = constant;

Complete solution isφ(xyz, x2 + y2 - 2z) = 0, where φ is an arbitrary function.

If A is \(\left[ {\begin{array}{*{20}{c}} 8&5\\ 7&6 \end{array}} \right]\) then the value of |A¹²¹- A¹²⁰|

Answer (Detailed Solution Below)

Option 1 : 0

Concept:

Let B = |A¹²¹- A¹²⁰|

B = |A¹²⁰ × (A – I)|

B = |A¹²⁰| × |A – I|

Calculation:

A =\(\left[ {\begin{array}{*{20}{c}} 8&5\\ 7&6 \end{array}} \right]\)

Now, calculating matrix [A – I]

[A – I] = \(\left[ {\begin{array}{*{20}{c}} 8&5\\ 7&6 \end{array}} \right] - {\rm{\;}}\left[ {\begin{array}{*{20}{c}} 1&0\\ 0&1 \end{array}} \right]\)

[A – I] = \(\left[ {\begin{array}{*{20}{c}} 7&5\\ 7&5 \end{array}} \right]\)

Now determinant of |A – I|,

|A – I| = \(\left| {\begin{array}{*{20}{c}} 7&5\\ 7&5 \end{array}} \right|\)

|A – I| = 0 (Since two rows are repeated, therefore determinant = 0)

Hence, |A¹²¹- A¹²⁰ | = 0

A matrix X has a dimension of 2 × 2. If the eigenvalues of this matrix is 5 and 6, what would be the eigen values of X²?

2.5 and 3
5 and 6
10 and 12
25 and 36

Answer (Detailed Solution Below)

Option 4 : 25 and 36

Concept:

If A is any square matrix of order n, we can form the matrix [A – λI], where I is the nth order unit matrix. The determinant of this matrix equated to zero i.e. |A – λI| = 0 is called the characteristic equation of A.

The roots of the characteristic equation are called Eigenvalues or latent roots or characteristic roots of matrix A.

Properties of Eigenvalues:

(1) If λ is an eigenvalue of a matrix A, then λn will be an eigenvalue of a matrix An.

(2) If λ is an eigenvalue of a matrix A, then kλ will be an eigenvalue of a matrix kA where k is a scalar.

(3) Sum of eigenvalues is equal to the trace of that matrix.

(4) The product of Eigenvalues of a matrix A is equal to the determinant of that matrix A.

(5) If λ is an Eigenvalue of matrix A, then λ2 will be an Eigenvalue of matrix A2.

(6) If λ1 is an Eigenvalue of matrix A, then (λ1 + 1) will be an Eigenvalue of the matrix (A + I).

(7) Eigenvalues of a matrix and its transpose are the same because the transpose matrix will also have the same characteristic equation.

Calculation:

If λ1, λ2, λ3 …. λ4 are the given values of A, then

eigenvalues of Amwill be\(\lambda _1^m,\lambda _2^m,\lambda _3^m, \ldots \ldots ..\)

'S' matrix has eigenvalues 5 and 6.

S2 matrix has eigenvalues 52 and 362

i.e. 25 and 36.

The approximate solution of the system of simultaneous equations

2x - 5y + 3z = 7

x + 4y - 2z = 3

2x + 3y + z = 2

by applying Gauss-Seidel method one time (using initial approximation as x - 0, y - 0, z - 0) will be:

x = 2.32, y = 1.245, z = -3.157
x = 1.25, y = -2.573, z = -3.135
x = 2.45, y = -1.725, z = -3.565
x = 3.5, y = -0.125, z = -4.625

Answer (Detailed Solution Below)

Option 4 : x = 3.5, y = -0.125, z = -4.625

Concept:

Gauss Seidel Method:

In Gauss Seidel method, the value of x calculated is used in next calculation putting other variable as 0.

2x - 5y + 3z = 7

Putting y = 0, z = 0 ⇒ x = 3.5

x + 4y - 2z = 3

Putting x = 3.5, z = 0 ⇒ y = - 0.125

2x + 3y + z = 2

Putting x = 3.5 , y = - 0.125 ⇒ z = 2 – 3(-0.125) – 2(3.5)

z = - 4.625

The value of\(\mathop \oint \nolimits_c \frac{1}{{{z^2} + 4}}dz\) Where C |z - 2i| = 1 is will be:

0
1/5
π/2
π /3

Answer (Detailed Solution Below)

Option 3 : π/2

Concept:

Cauchy's Integral Formula

If f(z) is analytic within and on a closed curve and ifais any point within C, then:

\(\mathop \smallint \limits_C^{} \frac{{f\left( z \right)}}{{z - a}}dz = 2\pi if\left( a \right)\)

Analysis:

Given:

\(f\left( z \right) = \smallint \frac{{{1}}}{{{z^2+4}}}dz\)

|z - 2i| = 1

|x + iy - 2i| = 1

|x + i(y - 2)| = 1

Taking the magnitude of the above, we get:

x2 +(y - 2)2= 1

This is the equation of a circle with:

Radius (r) = 1

Center = (0, 2)

Poles of f(z) = z² + 4

z = (+2i, -2i)

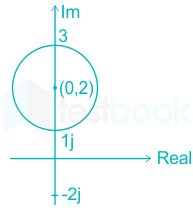
2i lies Inside the circle

-2i lies outside the circle

∴ We can write:

\(For\;pole\;\left( {z\; = \;-2i} \right) = \smallint \frac{{{1}}}{{\left( {z-2i} \right)\left( { z+2i} \right)}}dz = 0\)

Now, for pole z = 2i (lies inside the circle)

\(\smallint \frac{{{1}}}{{\left( {z+2i} \right)\left( {z-2i} \right)}}dz = 2\pi i{\left[ {\frac{{{1}}}{{2i+2i}}} \right]_{z = 2i}}\)

\(2\pi i\left[ {\frac{1}{4i}} \right] ={\frac{\pi}{2}}\)